Physics 480/581: Einstein's Relativity
Spacetime Diagrams


I.  Spacetime Diagrams

When considering events involving more than one observer, a very useful device for ``keeping track'' of all observations is the concept of a spacetime diagram, also called a ``Minkowski diagram,'' after the physicist who first used this scheme.

We agree to allocate to each observer, say S, a graph with vertical and horizontal axes. Our observer measures the coordinates of an event and locates them on the graph. He uses the vertical axis as a ``coordinate axis" for the values of ct for any event, as measured by S. He uses the horizontal axis as a ``coordinate axis'' for the values of x for the same event, also of course measured by S. This gives each event some point on the graph. [Since space really is 3-dimensional and not just 1-dimensional, occasionally we will need more than one dimension of the sort we usually think of as space. In such a case we would also put y and z here, all perpendicular to the vertical axis and, of course, perpendicular to each other. For two spatial coordinates this is only difficult and we will have to do it occasionally. In the case of needing three spatial coordinates it is impossible to draw; therefore, in those cases we will simply have to imagine it. They will probably not ever be needed.]

The worldline of an object is the set of all events at which that object is present. For instance, our observer, S's worldline is simply the vertical axis. Any object that S measures to be at rest will also have a vertical worldline, through, in general, some other point on the horizontal axis. An object that S measures to have constant velocity v will have a worldline that is straight but slanted at some angle. Since v = dx/dt = c(dx/c dt), the slope of that object's worldline will be c/v, i.e., the tangent of the angle, $\theta$, that the line makes with the horizontal axis will be such that

\begin{displaymath}\tan\theta = c/v \;.\end{displaymath} (1)

It therefore follows that the set of events that correspond to the passage of a (single) light ray--which moves at speed c--will be a straight line at $\pm 45^\circ$ to the horizontal axis. The two allowed angles correspond to moving in the $+\hat x$-direction or the $-\hat x$-direction. More generally, if we turn on a flashlight the rays will propagate outward in all directions. Thinking only about the $\hat x$- and $\hat y$-directions, this would generate not just the two rays at $\pm 45^\circ$ but an entire cone of rays all at $45^\circ$ to the vertical (or the horizontal). This cone is often referred to as the lightcone. Even when we need to consider all three spatial directions, we will still refer to the set of all these rays as the lightcone, even though it is now a cone in 4-dimensional spacetime.

The worldline of an object that is not moving at constant velocity, i.e., is accelerating, will not be a straight line, but will curve according to the acceleration. However, since no object may move at a speed greater than c, at all times the worldline of an object makes an angle with the horizontal that is greater than or equal to $\bf 45^\circ$. Of course we have equality only when the object is allowed to move at speed c, which mean that it would have zero mass, such as light.

Now consider the horizontal axis (or x-axis) of our observer S's Spacetime diagram. Those points correspond to all those events which S measures to have occurred at the time t=0; we may describe those events as a line of simultaneity for S. Another line of simultaneity for S would be any other line parallel to the x-axis, such as the line indicating all those events which occurred at, for instance, t = 2 nanoseconds, or, if you prefer, ct = 0.6 meters. The relationship between these two lines, i.e., these two lines of simultaneity for S is the same as between two worldlines of objects both of which S measures to be at rest.

We now need to broaden our ``horizons,'' and consider how S would describe quantities measured by another observer, S', who we take to be moving at some speed 0 < v < c. For simplicity, we assume that our two observers have synchronized their clocks and their (spatial) origins; i.e., they passed one another and both set their clocks to zero at that time. Therefore, we know that her worldline is a line through the origin with a slope of c/v. We know this simply from our understanding of worldlines. However, it is interesting to see it in a more algebraic way. Surely we also agree that the worldline of S' corresponds to the set of all events for which x' = 0. However, the Lorentz transformation equations tell us that $x' = \gamma(x-vt)$. Therefore we can immediately see that the location x'=0 corresponds to the graph x = vt, or, since we have ct plotted along the vertical axis, the equation should be given in the form ct = (c/v) x. This is indeed a straight line (through the origin) with slope c/v, as expected. Since this line is indeed the worldline of the observer S', we could also consider this line, the worldline of S', as the ct'-axis; i.e., it is the set of points along which the values of ct' vary while the values of x'remain fixed, and fixed at x'=0. It would therefore be reasonable that lines parallel to this axis correspond to worldlines of objects that S' measures to be at rest, in her frame; i.e., they would have fixed, but non-zero, values for x'.

Utilizing that algebraic approach, we may now inquire as to the shape of a line of simultaneity for this new observer S'. Taking, for instance, the time t'=0, this line of simultaneity must correspond to all the points that have t'=0. However, again, the Lorentz transformation equations tell us that $t' = \gamma(t-vx/c^2)$. Setting t'=0 gives us the equation ct = (v/c) x, which is a straight line (through the origin) with the ``opposite'' slope, i.e., with $\tan\theta = v/c$. If the worldline of S' makes an angle $\phi$ with respect to the ct-axis--with $\tan\phi = v/c$, then the t'=0 line of simultaneity also makes an angle of $\phi$, but with respect to the x-axis. Again, since this line corresponds to all the events which have t'=0, but which have varying values of x', we may consider it as the x'-axis. Then, lines parallel to this line, i.e., parallel to the x'-axis, would be other lines of simultaneity, with fixed, but non-zero, values for t'. We may summarize the statements above as follows:

Below we show a figure that shows the axes of S' as measured by S, i.e., as shown on the Spacetime diagram for S. On the graph we have chosen the speed of S' as v = 0.6 c. Notice that the associated value for $\gamma = 1/\sqrt{1-(v/c)^2}$ is $\gamma = 1.25$.


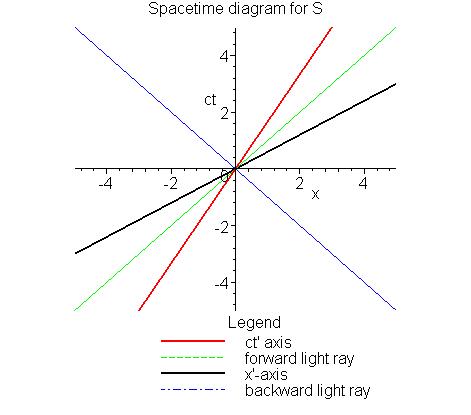
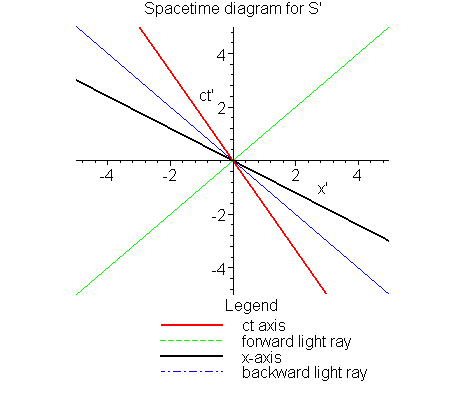
It would be reasonable to ask what does the Spacetime diagram for S' look like, and, in particular, what do the axes of the observer S look like on that diagram. From the point of view of S' the observer S is moving with constant speed, -v. Therefore we may use the inverse Lorentz transformations to determine quickly what these axes look like, in S'-land:

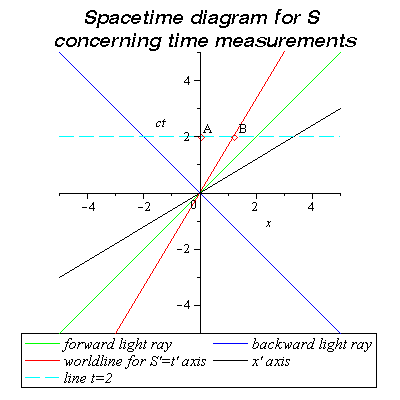
We show this new graph below, where now S is traveling with the speed v = -0.6 c, as measured by S':


Now, we come to the most perplexing feature of Spacetime diagrams, unfortunately. If we consider, for instance, time passed in frame S', we know that since S' is moving her time should move less rapidly than time as measured in S. However, now we look at the graph of S's Spacetime diagram. Since the graph of the ct'-axis, i.e., the worldline of S', is slanted, what appears to be the ``distance'' along that slanted line would be longer than a corresponding distance along the vertical line which is the worldline for S.

Let us be more precise. We first look at the event where S is 2 hours older than he was when the origin was established, i.e., the event on the ct-axis marked by the symbol 2. (For convenience we will label this event as A, on the figure shown below.) Then we draw a line parallel to his x-axis through this point, i.e., a horizontal line through the point (x,ct) = (0,2). This line constitutes a line of simultaneity for S, of all events that he measures as happening at exactly the same time as his being 2 hours older. This cuts the worldline for S' at a point satisfying x=(v/c)t, the equation for the worldline belonging to S'. We will label this event as B.


On our diagram this means that for B we have x = (0.6)2 = 1.2 light-hours. At this event, on the worldline for S', our observer S measures the values (x,t) = (1.2,2). This is an event that S believes to be simultaneous with his being 2 hours older. However, we would like very much to know what values S' associates with this event, B. Particularly, we would like to know how much older is S' at this event. At the moment, our only recourse is to use the Lorentz transformation equations to tell us; they say that

\begin{eqnarray*}x' = \gamma(x - v t)& = & 1.25[1.2 - .6(2)] = 0\;,\\ [2pt] t' = \gamma(t - vx/c^2)& = & 1.25[2 - .6(1.2)] = 1.6 \hbox{~hours.} \end{eqnarray*}


Therefore at event B, S' measures that she has aged only t' = 1.6 hours since their mutual meeting, back when they synchronized their origins and clocks, the event O. Notice that the equations also tell us the (expected) result that x'=0 for event B; i.e., this is indeed a point on the worldline for S'. This is in complete agreement with what we expected.

This result is nonetheless in rather strong disagreement with what we might have expected by simply ``looking at'' the Spacetime diagram that S has constructed. On the piece of paper for that diagram, we see event B as lying along this slanted line from the origin and therefore ``obviously'' further away from the origin than event A. The fact that this ``obvious result'' is in disagreement with our calculations is the source of our difficulty. Of course our ``obvious'' perceptions are based on our use of the usual, Pythagorean method of measuring distance, via the length for the hypotenuse of a triangle. However, in this case, that triangle has one ``leg'' which is a spatial distance, and another ``leg'' which is a temporal distance, i.e., a time. Even though we have multiplied that time by the constant c to make the units the same, they are still quite different concepts. Therefore, in fact we have no justification for believing that we may still use the (Pythagorean) rule for calculation of the lengths of hypotenuses to obtain a true measure of distance. Since the diagram is drawn on a piece of paper where we usually deal with x and y, rather than x and ct, our eye is misled. We may certainly rephrase this difficulty in the following way:

Distance on a Spacetime diagram, with coordinates x and ct,
does NOT use the same distance as would x and y,
on a normal sheet of paper.
We now begin an explanation of this important notion, which will tell us that an appropriate notion of ``distance'' in spacetime will be the relativistic interval, which, in the simplest cases, has the form x2 - (ct)2 instead of the Pythagorean form, x2 + y2.

II.  the (Lorentz) Invariant Interval

A very important feature of ordinary distance is its property of invariance under changes of observer. It is this property that we can still preserve in our Spacetime diagram when we are composing quantities involving both spatial distances and temporal distances. To begin, let us first describe the invariance of ordinary spatial distances, considering only 2-dimensional geometry, where we know that Pythagoras' Theorem is true. We then consider two different observers--both at rest--but with different choices of coordinate axes--say, rotated one with respect to the other. For some pair of locations, these observers measure different values for the x-coordinates and the y-coordinates of the two locations being considered. Nonetheless, they still agree on the value of the distance between the two locations. This is a reason that distance is so important, namely that it is a quantity that is independent of the particular observer who measures it, even though this those observers measure different values for the respective coordinates.

The (relativistic, invariant) interval is a generalization of the usual (Pythagorean) distance between two points which takes proper care of the fact that there is a distinct difference between spatial coordinates and temporal coordinates. For any pair of events, the following function of the coordinate differences between them is independent of the choice of (inertial) observer:

\begin{displaymath}(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2 - (c\,\Delta t)^2... ... (c\,\Delta t^{{{\lower1.1pt\hbox{{\ponts /}}}\!\!}})^2 \quad. \end{displaymath} (2)

Because of the minus sign in the definition of the interval, for different pairs of events, it can be positive, zero, or negative, although every observer in every reference frame will agree on that value! Since there are these various possibilities, they each have a name attached, and we will now discuss each one briefly: spacelike, lightlike, and timelike. [This important notion is not discussed in your text.]

(a) 
Spacelike Separation for 2 Events $\Longleftrightarrow \hbox{\bf I} > 0\ $:As a first event, we consider the landing of an airplane at the Albuquerque airport at 10 a.m.; as the second event we consider the landing of a different airplane at the airport in Washington, D.C., at 12 noon. The United States has a pre-established system of time zones that arranges for 12 noon in Washington, D.C. to be the same time as 10 a.m. in Albuquerque. Therefore, we say that these two events are simultaneous as measured in the reference frame of the United States Federal Aviation Authority. (We ignore the rotation of the earth, as usual.) Therefore, $\Delta t = 0$, and the value of the interval is surely positive for these two events.

The value of I is simply the square of the (usual, Pythagorean) direct distance between Washington, D.C. and Albuquerque. Other observers, such as a communications satellite moving overhead might disagree--at least slightly--about the value of the length and whether the two events were simultaneous, but they will agree on the value of I.
(b) 
Lightlike Separation for 2 Events $\Longleftrightarrow \hbox{\bf I} = 0\ $:Our first event is the initial sending out of a radio signal, from White Sands Missile Range, to a spaceship cruising near Mars; the second event is the reception of that signal by the spaceship near Mars. The time required for the radio signal to travel there would simply be the distance, as measured in the Earth's reference frame, divided by the speed of light, c. Therefore, the value of the interval will be exactly zero! All observers will agree on this zero value for the interval since all of them will agree on the value of the speed of light, even though they may differ on the numerical values of the length and time.
(c) 
Timelike Separation for 2 Events $\Longleftrightarrow \hbox{\bf I} < 0\ $:Here our first event will be the arrival of Coronado on the banks of the Rio Grande River, a little south of Bernalillo, where ``Old Town'' in the city of Albuquerque would someday be; the second event is the lighting of the luminarias last Christmas Eve in ``Old Town.'' These 2 events occurred at the same place (to within our level of accuracy) so that $\Delta x = 0$, $\Delta y = 0$, and $\Delta z = 0$; however, there was a time difference of a few hundred years, so that it is clear that the the interval I has a negative value, of a few hundred light-years. Again, other observers might well measure different values for the differences of the coordinates, but they would agree on the value of the interval.


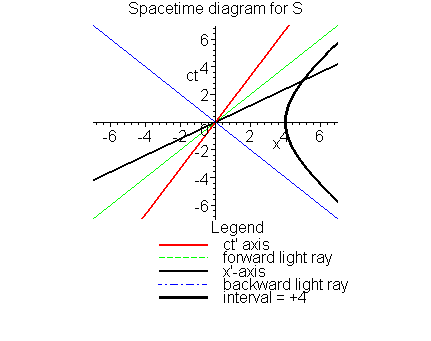
We can now use the interval to create a new method to visualize its values on a Spacetime diagram. Let us return to the consideration of point A and B on the Spacetime diagram that belongs to S. Point A had the coordinates (x,ct) = (0,2). Therefore the value of the interval (relative to the origin) for that point is just 02 - 22 = -4 (light-hours)2. There is then a hyperbola that we may draw on the spacetime diagram that goes through that point, namely

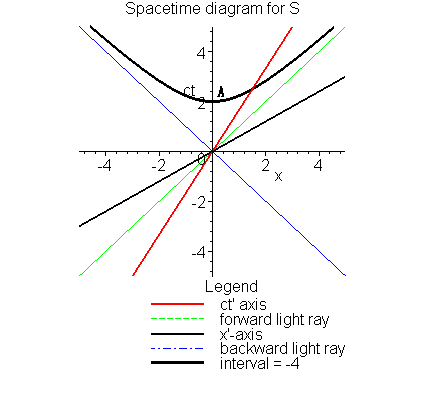
\begin{displaymath}x^2 - (ct)^2 = -4 = (x')^2 - (ct')^2 \;. \end{displaymath}

Not only does the second equality tell us that all observers will agree on this value for that point, but it will allow us to calibrate distances along the worldline (and lines of simultaneity) for S'. The point at which this hyperbola intersects the worldline for S' is a third point to consider. We will label it event C, and notice that it lies further along that worldline than did our earlier event B. Since event C lies on the worldline for S', then it has x'=0; since it also lies on the hyperbola for the interval ${\bf I} = -4$ then it must have ct' = 2 hours. So event C is that particular event where this other observer, S', has aged 2 hours since the earlier meeting of S and S'. Looking just at the line on the piece of paper, between the origin and event C, that line appears to be longer than the line between the origin and event A, which is where S had aged 2 hours since their meeting. Therefore, we see that our perception of distances on the piece of paper is NOT particularly well related to actual distances measured by our different observers. Instead, we may use the hyperbolae generated by constant values of the invariant interval to create scales for our perception of distance.

At every point where a given hyperbola (for a timelike event) intersects some observers's worldline, that observer will measure the same time in his or her frame.
So on our graph the event A on the hyperbola corresponds to the measurement by S of a time passed of t = 2 hours, and the event C, also on the hyperbola, corresponds to the measurement by S' of a time passed of t' = 2 hours. We now note that event C occurred after event B. Since B was simultaneous with A, in the frame of S, we can infer that at the time that A was aged 2 hours more, his measurement of S' was that she was aged less than that!

Quite a different interpretation may be made if we switch to the Spacetime diagram for S'. On this diagram, we may locate the event C, which is where she had aged 2 hours since their origins coincided. We may then draw the same hyperbola as before through this point, but now we draw on the Spacetime diagram for S'. It intersects the worldline for S at the point A.

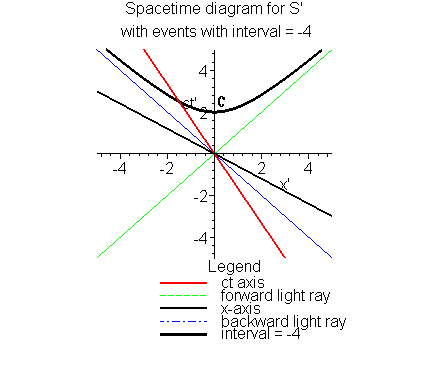
On this diagram we may also draw a line of simultaneity for S', i.e., a line parallel to her x'-axis and through event C. We easily see that it intersects the worldline of S at an earlier point, which we now call D. At the point D, S is clearly younger than at the point A, since it occurs earlier on his worldline; therefore, as measured by S', the observer S is younger than she is. From the general principles, this is consistent since, after all, she measures S as moving!

The interval may also be used to determine calibrations for distances along curves which lie in the spacelike region of spacetime. An important example of this is a set of points that are measured as simultaneous by some particular observer, usually moving as seen by our initial observer, S. We begin with a point on S's x-axis, which is, say, 10 meters away from the origin. As measured by S', this point has an interval with value $(\Delta x)^2 - (c\Delta t)^2 = +100$, since it is simultaneous with the origin as he measures it. Therefore, if we now consider the hyperbolic curve

(x)2 - (c t)2 = 102 = + 100 = (x')2 - (c t')2,

this curve lies, at all points, within the region of spacetime that is spacelike-separated relative to the origin. (It asymptotically approaches the light cone for S, but never actually touches it.) We want to use this hyperbola to determine values for x', the coordinate values for S' We begin by noting that the Lorentz transformation equations tells us that the x'-axis, i.e., the set of all points for which ct' = 0, is given--in the coordinates used by S, and therefore appropriate for a graph on the Spacetime diagram used by S--by the equation x = vt = (v/c)(ct), which is a straight line through the origin and having a slope of v/c relative to the positive x-axis. Our current task is to calibrate distances along this x'-axis, as measured by S' , i.e., in coordinates x', but displayed by S, i.e., on his Spacetime diagram. This is straightforward, and works in just the same way as it did for the ct'-axis of S'. Since the invariant interval has the same value for any observer, when the hyperbola described above crosses the x'-axis it has coordinate ct'=0, so that the value of x' is exactly 10 meters. Of course looking at the diagram, in the coordinates for S, it appears that this intersection occurs at a distance farther away from the origin than does the intersection with the x-axis. As we already know, by studying the timelike cases, this is simply a ``difficulty'' with the measurement of distances on a Spacetime diagram, and there is nothing we can do about it, but learn how to correctly calibrate the ``tickmarks'' along the various axes. In particular, if we now construct an entire sequence of such hyperbolae, for instance, intersecting the x-axis at the values of 10, 20, 30, 40, and 50 meters, then their intersection points with the x'-axis correspond to points which have the coordinate values x'=10, x'=20, x'=30, x'=40and x'=50 meters; of course all of them have the coordinate value ct' = 0 meters.
The graph below shows the spacelike hyperbola for I = +(4)²:

III.   Use of light rays to further determine distances

In this section we first recall that S and S' have coordinated their origins and synchronized their clocks, and that S has measured the velocity of S' to be v = 0.6c, from which he calculates that her relativistic factor is $\gamma = 1.25$. At this time, they arrange that they will send light rays (electromagnetic signals) to one another, and keep good records of when these signals were received, and sent. Our observer S' sends out a light ray (backward) toward S when her clocks tell her that it has been 1 year since they met. We call that event A, and it obviously has coordinates x' = 0 and ct' = 1 year. Using the Lorentz transformation equations, we may also determine its coordinates as measured by S:

\begin{displaymath}x = 1.25[0 + (0.6)(1)] = 0.75\ \hbox{lt-yrs and~~} ct = 1.25[1 + 0] = 1.25\hbox{~lt-yrs.} \end{displaymath}

We indicate the path of this light ray by drawing a line at 45$^\circ$ (to the x- and also ct-axes, that heads toward the left until it strikes the ct-axis, i.e., until it is received by S. The light ray must therefore travel a distance of 0.75 lt-yrs, at the speed of light, which requires 0.75 years. Therefore, it arrives back at the location of S at the time t = 2 years, which we refer to as the event B. The (inverse) Lorentz transformation equations again give us

\begin{displaymath}x' = 1.25[0 - (0.6)(2)] = - 1.5\hbox{~lt-yrs, and~~} ct' = 1.25[2 - (0.6)0] = 2.5\hbox{~lt-yrs.} \end{displaymath}

Immediately S sends back a light signal to S', saying that the signal has been received. Of course S' has been traveling further away all this time, so this (second) light ray will have further to travel than did the one coming the other way. There are several different ways to calculate how long this second light ray will take. Let us use the following approach. Knowing that event B is 1.5 lt-yrs away from S', and that it occurred at ct' = 2.5 lt-yrs, we may simply follow it back, at the speed of light, to the location of S', which is always fixed at x' = 0. Having traveled for 1.5 years to arrive back there, the event, C, of its reception will have primed coordinates x' = 0 and ct' = 4 lt-yrs. Transferring, now, one last time back to the coordinates used by S, we may calculate

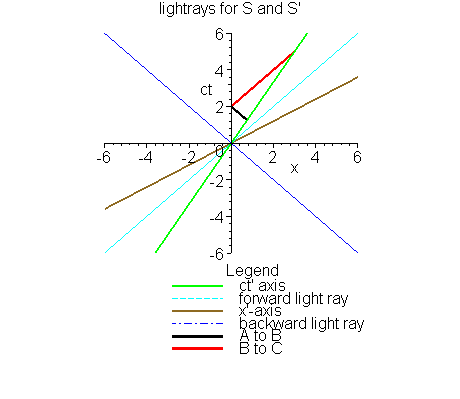
\begin{displaymath}x = 1.25[0 + (0.6)4] = 3 \hbox{~lt-yrs, and~~} ct = 1.25[4 + (0.6)(0)] = 5 \hbox{~lt-yrs.} \end{displaymath}

[On the graph, points A, B, and C are not labeled. But the short (black) lightray travels from A (backward) to B, while the longer (red) lightray travels from B (forward) to C.]
At this time S' has aged 4 years and has arrived at a place that S measures to be 3 lt-yrs away, it having of course taken her 5 years as measured by S. This is the end of this particular episode.

Daniel Finley